Projects
Adaptive Neural Tensor Networks for parametric PDEs
Abstract
The project is concerned with the reliable neural network (NN) approximation of solutions for high-dimensional PDEs. While NNs have become quite popular in the scientific computing community, experimental results often exhibit a flattening convergence behavior despite well-known theoretical expressivity results of the employed architectures. In order to better understand this observation and to alleviate the practical implications, our focus lies on two key challenges.
First, strategies to include information about the physical model have to be examined. The compliance with such constraints might provide an indication about how to construct a network topology that is better adapted to the requirements of the model. As an optimal scenario, an iterative refinement algorithm based on some error estimator can be developed. The obtained results are planned to also be adopted to invertible NNs.
Second, the training process is notoriously difficult and might benefit from connections that can be drawn to tree-based tensor networks (TN). These provide a rich mathematical structure and might prove useful as pre-conditioners for NNs, leading to a more robust training of NN parameters. Moreover, the combination of these two network architectures could lead to promising new class of approximation methods which we (optimistically) coin neural tensor networks (NTN). These could for instance resemble a typical NN structure with layers of hierarchical low-rank tensor components.
Participants
- Prof. Dr. Martin Eigel
- Prof. Dr. Lars Grasedyck
- Janina Schuette
Assessment of Deep Learning through Meanfield Theory
Abstract
Kinetic and meanfield theory have proven an useful mathematical tool for hierarchical scale modeling of a variety of physical and sociological processes. It in particular allows to study emergent behavior as consequence of particle--to--particle dynamics. Modern learning methods can mathematically be reformulated such that a particle interaction structure emerges. E.g.~the class of residual deep neural networks in the limit of infinitely many layer leads to a coupled system of ordinary differential equations for the activation state of neurons. This arising system can be reformulated as an interacting 'particle' system where the state of each particle corresponds to the activation state of a neuron at a certain point in time. Within this proposal, we aim to exploit and extend existing meanfield theory to provide a mathematical framework for modern learning methods that allow for this description and hence focusing on learning by deep neural networks and learning through filtering methods. Methods from kinetic and meanfield theory will be extended in order to gain insight on properties and mechanisms of those learning approaches. The gained insight will used to propose novel, provable convergent and stable methods to solve learning problems.
Participants
- Prof. Dr. Michael Herty
- Dr. Chiara Segala
- Dr. Giuseppe Visconti
Combinatorial and implicit approaches to deep learning
Abstract
This project develops mathematical methods for studying neural networks at three different levels: the individual functions represented by the network, the function classes, and the function classes together with a training objective. On the one hand, we seek
to describe the combinatorics of the functions represented by a neural
network given a particular choice of the parameter or a distribution
of parameters. On the other hand, we investigate implicit
characterizations of the function classes that can be represented by a neural network over a given training set. We use these to investigate the role of the training data and the properties of the parameter optimization problem when training neural networks.
Participants
- Prof. Dr. Guido Montúfar
Curse-of-dimensionality-free nonlinear optimal feedback control with deep neural networks
Abstract
Optimal feedback control is one of the areas in which methods from deep learning have an enormous impact. Deep Reinforcement Learning, one of the methods for obtaining optimal feedback laws and arguably one of the most successful algorithms in artificial intelligence, stands behind the spectacular performance of artificial intelligence in games such as Chess or Go, but has also manifold applications in science, technology and economy. Mathematically, the core question behind this method is how to best represent optimal value functions, i.e., the functions that assign the optimal performance value to each state, also known as cost-to-go function in reinforcement learning, via deep neural networks (DNNs). The optimal feedback law can then be computed from these functions. In continuous time, these optimal value functions are characterised by Hamilton-Jacobi-Bellman partial differential equation (HJB PDEs), which links the question to the solution of PDEs via DNNs. As the dimension of the HJB PDE is determined by the dimension of the state of the dynamics governing the optimal control problem, HJB equations naturally form a class of high-dimensional PDEs. They are thus prone to the well-known curse of dimensionality, i.e., to the fact that the numerical effort for its solution grows exponentially in the dimension. It is known that functions with certain beneficial structures, like compositional or separable functions, can be approximated by DNNs with suitable architecture avoiding the curse of dimensionality. For HJB PDEs characterising Lyapunov functions it was recently shown by the proposer of this project that small-gain conditions - i.e., particular conditions on the dynamics of the problem - establish the existence of separable subsolutions, which can be exploited for efficiently approximating them by DNNs via training algorithms with suitable loss functions. These results pave the way for curse-of-dimensionality free DNN-based approaches for general nonlinear HJB equations, which are the goal of this project. Besides small-gain theory, there exists a large toolbox of nonlinear feedback control design techniques that lead to compositional (sub)optimal value functions. On the one hand, these methods are mathematically sound and apply to many real-world problems, but on the other hand they come with significant computational challenges when the resulting value functions or feedback laws shall be computed. In this project, we will exploit the structural insight provided these methods for establishing the existence of compositional optimal value functions or approximations thereof, but circumvent their computational complexity by using appropriate training algorithms for DNNs instead. Proceeding this way, we will characterise optimal feedback control problems for which curse-of-dimensionality-free (approximate) solutions via DNNs are possible and provide efficient network architectures and training schemes for computing these solutions.
Participants
- Prof. Dr. Lars Grüne
- Mario Sperl
Deep assignment flows for structured data labeling: design, learning and prediction performance
Abstract
This project focuses on a class of continuous-time neural ordinary differential equations (nODEs) called assignment flows for labeling metric data on graphs. It aims to contribute to the theory of deep learning by working at the intersection of statistical learning theory, differential geometry, PDE-based image processing and game theoretical methods.
This encompasses three complementary viewpoints:
- use of information geometry for design and understanding the role of parameters in connection with learning and structured prediction;
- study of PAC-Bayes risk bounds for local predictions of weight parameter patches on a manifold and the implication for the statistical accuracy of non-local labelings predicted by the nODE;
- algorithm design for parameter learning based on a linear tangent space representation of the nODE, as a basis for linking statistical learning theory to applications of assignment flows in practice.
By extending the statistical theory of classification, a specific challenge of risk certification in structured prediction problems to be addressed in this project is to both quantify uncertainty as well as localize it. For instance, in image segmentation a goal is to combine a bound on the number of wrongly classified pixels with a faithful representation of confidence in pixelwise decisions to locate likely error sources.
Participants
- Prof. Dr. Christoph Schnörr
- Bastian Boll
Deep-Learning Based Regularization of Inverse Problems
Abstract
Deep learning has attracted enormous attention in many fields like image processing and consequently it receives growing interest as a method to regularize inverse problems. Despite its great potential, the development of methods and in particular the understanding of deep networks in this respect is still in its infancy. We hence want to advance the construction of deep-learning based regularizers for ill-posed inverse problems and their theoretical foundations. Particular goals are the development of robust and interpretable results, which enforce to develop novel concepts of robustness and interpretability in this setup. The theoretical developments will be accompanied by extensive computational tests and the development of measures and benchmark problems for fair comparison of different approaches.
Participants
- Prof. Dr. Martin Burger
- Prof. Dr. Gitta Kutyniok
- Yunseok Lee
Deep learning for non-local partial differential equations
Abstract
High-dimensional partial differential equations (PDEs) with non-local terms arise in a variety of applications, e.g., from finance and ecology. This project studies deep learning algorithms for such PDEs both from a theoretical and practical perspective.
Participants
- Prof. Dr. Lukas Gonon
- Prof. Dr. Arnulf Jentzen
Deep neural networks overcome the curse of dimensionality in the numerical approximation of stochastic control problems and of semilinear Poisson equations
Abstract
a. Partial differential equations (PDEs) are a key tool in the modeling of many real world phenomena. Several PDEs that arise in financial engineering, economics, quantum mechanics or statistical physics are nonlinear, high-dimensional, and cannot be solved explicitly. It is a highly challenging task to provably solve such high-dimensional nonlinear PDEs approximately without suffering from the so-called curse of dimensionality. Deep neural networks (DNNs) and other deep learning-based methods have recently been applied very successfully to a number of computational problems. In particular, simulations indicate that algorithms based on DNNs overcome the curse of dimensionality in the numerical approximation of solutions of certain nonlinear PDEs. For certain linear and nonlinear PDEs this has also been proven mathematically. The key goal of this project is to rigorously prove for the first time that DNNs overcome the curse of dimensionality for a class of nonlinear PDEs arising from stochastic control problems and for a class of semilinear Poisson equations with Dirichlet boundary conditions.
Participants
- Prof. Dr. Martin Hutzenthaler
- Prof. Dr. Thomas Kruse
Globally Optimal Neural Network Training
Abstract
The immense success of applying artificial neural networks (NNs) builds fundamentally on the
ability to find good solutions of the corresponding training problem. This optimization problem
is non-convex and usually solved for huge-scale networks. Therefore, typically local methods
like stochastic gradient descent (SGD) and its numerous variants are used for training. To assess
the quality of the produced solutions, globally optimal ones are needed. This is the central
motivation of this project, whose core idea is to develop and investigate methods for computing
globally optimal solutions of the training problem using techniques from Mixed-Integer Nonlinear
Programming (MINLP).
To support generalizability and explainability as well as to improve the performance, we will
also investigate two other important properties of neural networks: sparsity and symmetry. Both
need to be incorporated into an exact optimization approach in order to obtain a theoretical and
practical understanding of its possibilities and limits.
Participants
- Prof. Dr. Marc Pfetsch
- Prof. Dr. Sebastian Pokutta
- Jeremy Jany
Implicit Bias and Low Complexity Networks (iLOCO)
Foundations of Supervised Deep Learning for Inverse Problems
Abstract
Over the last decade, deep learning methods have excelled at various data processingtasks including the solution of ill-posed inverse problems. While many works have demonstrated thesuperiority of such deep networks over classical (e.g. variational) regularization methods in imagereconstruction, the theoretical foundation for truly understanding deep networks as regularizationtechniques, which can reestablish a continuous dependence of the solution on the data, is largelymissing. The goal of this proposal is to close this gap in three step: First we will study deep net-work architectures that map a discrete (finite dimensional) representation of the data to a discreterepresentation of the solution in such a way, that we establish data consistency in a similar way asdiscretizations of classical regularization methods do. Secondly, we will study how to design, interpretand train deep networks as mappings between infinite-dimensional function spaces. Finally, we willinvestigate how to transfer finite-dimensional error estimates to the infinite-dimensional setting, bymaking suitable assumptions on the data to reconstruct as well as the data to train the network with,and utilizing suitable regularization schemes for the supervised training of the networks themselves.We will evaluate our networks and test our finding numerically on linear inverse problems in imagingusing image deconvolution and computerized tomography as common test settings.
Participants
- Prof. Dr. Martin Burger
- Prof. Dr. Michael Möller
- Samira Kabri
- Lukas Weigand
Multilevel Architectures and Algorithms in Deep Learning
Abstract
The design of deep neural networks (DNNs) and their training is a central issue in machine learning. Progress in these areas is one of the driving forces for the success of these technologies. Nevertheless, tedious experimentation and human interaction is often still needed during the learning process to find an appropriate network structure and corresponding hyperparameters to obtain the desired behavior of a DNN. The strategic goal of the proposed project is to provide algorithmic means to improve this situation. Our methodical approach relies on well established mathematical techniques: identify fundamental algorithmic quantities and construct a-posteriori estimates for them, identify and consistently exploit an appropriate topological framework for the given problem class, establish a multilevel structure for DNNs to account for the fact that DNNs only realize a discrete approximation of a continuous nonlinear mapping relating input to output data. Combining this idea with novel algorithmic control strategies and preconditioning, we will establish the new class of adaptive multilevel algorithms for deep learning, which not only optimize a fixed DNN, but also adaptively refine and extend the DNN architecture during the optimization loop. This concept is not restricted to a particular network architecture, and we will study feedforward neural networks, ResNets, and PINNs as relevant examples. Our integrated approach will thus be able to replace many of the current manual tuning techniques by algorithmic strategies, based on a-posteriori estimates. Moreover, our algorithm will reduce the computational effort for training and also the size of the resulting DNN, compared to a manually designed counterpart, making the use of deep learning more efficient in many aspects. Finally, in the long run our algorithmic approach has the potential to enhance the reliability and interpretability of the resulting trained DNN.
Participants
- Prof. Dr. Anton Schiela
- Frederik Köhne
- Prof. Dr. Roland Herzog
Multi-Phase Probabilistic Optimizers for Deep Learning
Abstract
We will investigate a novel paradigm for the training of deep neural networks with stochastic optimization. The peculiarities of deep models, in particular strong stochasticity (SNR< 1), preclude the use of classic optimization algorithms. And contemporary alternatives, of which there are already many, are wasteful with resources. Rather than add yet another optimization rule to the long and growing list of such methods, this project aims to make substantial conceptual progress by using novel observables, in particular the probability distribution of gradients across the dataset to automatically set and tune algorithmic parameters. In doing so we will deviate from the traditional paradigm of an optimization method as a relatively simple update rule and describe the optimization process as a control problem with different phases.
Participants
- Prof. Dr. Philipp Hennig
- Frank Schneider
Multiscale Dynamics of Neural Nets via Stochastic Graphops
Participants
- Prof. Dr. Maximilian Engel
- Prof. Dr. Christian Kühn
- Dennis Chemnitz
- Sara-Viola Kuntz
On the Convergence of Variational Deep Learning to Sums of Entropies
Abstract
Our project investigates the convergence behavior for learning based on deep probabilistic data models. Models of interest include (but are not limited to) variational autoencoders (VAEs), deep Bayesian networks, and deep restricted Boltzmann machines (RBMs). Central to our investigations is the variational lower bound (a.k.a. free energy or ELBO) as a very frequently used and theoretically well-grounded learning objective. The project aims at exploring and exploiting a specific property of ELBO optimization: The converges of the ELBO objective to a sum of entropies, where the sum consists of (A) the (average) entropy of variational distributions, (B) the (negative) entropy of the prior distribution, and (C) the (expected and negative) entropy of the generating distribution. Entropy sums may become more complex with more intricate models. Convergence to entropy sums has been observed and analyzed for standard VAEs in preliminary work [1]. The project investigates the generalizability of the result and conditions under which the convergence property holds true. Furthermore, the project investigates (1) how convergence to entropy sums can be exploited to acquire insights into the learning behavior of deep models and to understand phenomena such as posterior collapse; and (2) how learning and learning objectives can themselves be defined to improve learning based on deep probabilistic models.
[1] "The Evidence Lower Bound of Variational Autoencoders Converges to a Sum of Three Entropies", J. Lücke, D. Forster, Z. Dai, arXiv:2010.14860, 2021.
Participants
- Prof. Dr. Asja Fischer
- Prof. Dr. Jörg Lücke
Provable Robustness Certification of Graph Neural Networks
Abstract
Graph Neural Networks (GNNs), alongside CNNs and RNNs, have become a fundamental building block in many deep learning models, with ever stronger impact on domains such as chemistry (molecular graphs), social sciences (social networks), biomedicine (gene regulatory networks), and many more. Recent studies, however, have shown that GNNs are highly non-robust: even only small perturbations of the graph’s structure or the nodes’ features can mislead the predictions of these models significantly. This is a show-stopper for their application in real-world environments, where data is often corrupted, noisy, or sometimes even manipulated by adversaries. The goal of this project is to increase trust in GNNs by deriving principles for their robustness certification, i.e. to provide provable guarantees that no perturbation regarding a specific corruption model will change the predicted outcome.
Participants
- Prof. Dr. Stephan Günnemann
- Jan Schuchardt
Solving linear inverse problems with end-to-end neural networks: expressivity, generalization, and robustness
Abstract
Deep neural networks have emerged as highly successful and universal tools for image recovery and restoration. They achieve state-of-the-art results on tasks ranging from image denoising over super-resolution to image reconstruction from few and noisy measurements. As a consequence, they are starting to be used in important imaging technologies, such as GEs newest computational tomography scanners.
While neural networks perform very well empirically for image recovery problems, a range of important theoretical questions are wide open. Specifically, it is unclear what makes neural networks so successful for image recovery problems, and it is unclear how many and what examples are required for training a neural network for image recovery. Finally, the resulting network might or might not be sensitive to perturbations. The overarching goal of this project is to establish theory for learning to solve linear inverse problems with end-to-end neural networks by addressing those three questions.
Participants
- Prof. Dr. Reinhard Heckel
- Prof. Dr. Felix Krahmer
Statistical Foundations of Unsupervised and Semi-supervised Deep Learning
Abstract
Recent theoretical research on deep learning has primarily focussed on the supervised learning problem that is, learning a model using labelled data and predicting on unseen data. However, deep learning has also gained popularity in learning from unlabelled data. In particular, graph neural networks have become the method of choice for semi-supervised learning, whereas autoencoders have been successful in unsupervised representation learning and clustering. This project provides a mathematically rigorous explanation for why and when neural networks can successfully extract information from unlabelled data. To this end, two popular network architectures are studied that are designed to learn from unlabelled or partially labelled data: graph convolutional networks and autoencoder based deep clustering networks. The study considers a statistical framework for data with latent cluster structure, such as mixture models and stochastic block model. The goal is to provide guarantees for cluster recovery using autoencoders as well as the generalisation error of graph convolutional networks for semi-supervised learning under cluster assumption. The proposed analysis combines the theories of generalisation and optimisation with high-dimensional statistics to understand the influence of the cluster structure in unsupervised and semi-supervised deep learning. Specifically, the project aims to answer fundamental questions such as which types of high-dimensional clusters can be extracted by autoencoders, what is the role of graph convolutions in semi-supervised learning with graph neural networks, or what are the dynamics of training linear neural networks for these problems.
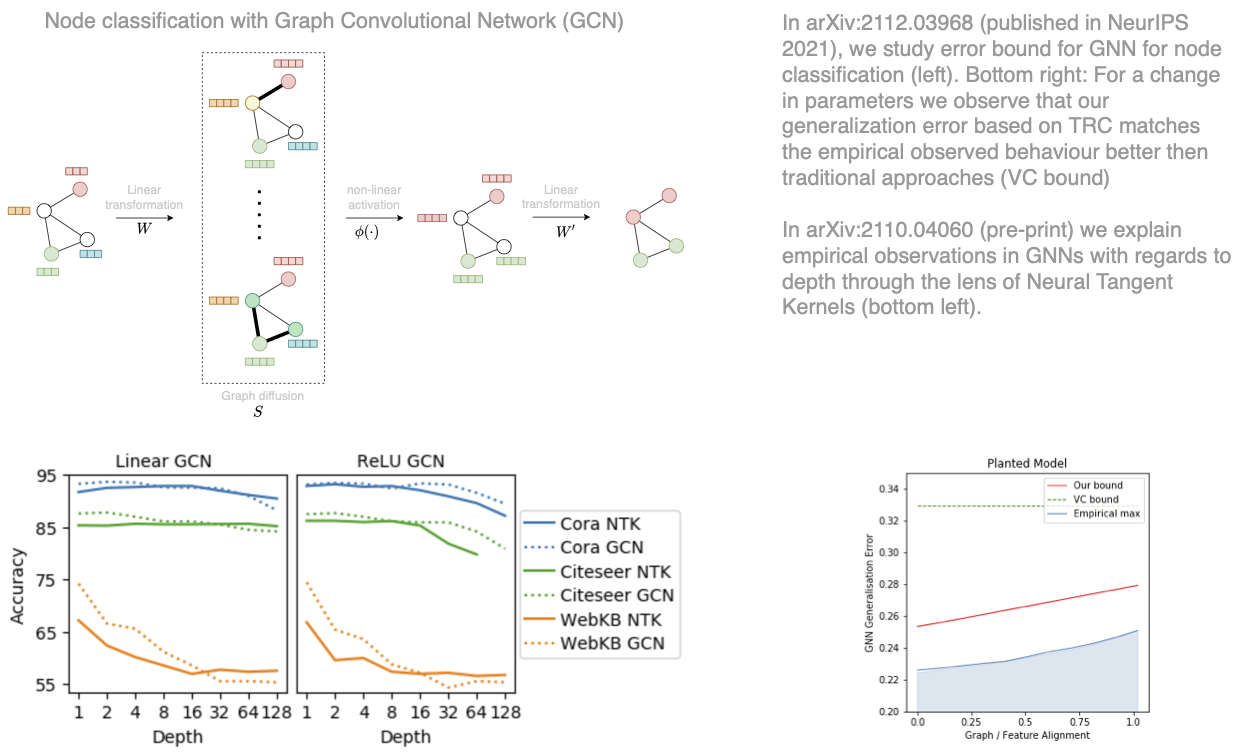
Participants
- Prof. Dr. Debarghya Ghoshdastidar
- Pascal Esser
Structure-preserving deep neural networks to accelerate the solution of the Boltzmann equation
Abstract
The goal of this project is to use deep neural networks as building blocks in a numerical method to solve the Boltzmann equation. This is a particularly challenging problem since the equation is a high-dimensional integro-differential equation, which at the same time possesses an intricate structure that a numerical method needs to preserve. Thus, artificial neural networks might be beneficial, but cannot be used out-of-the-box.
We follow two main strategies to develop structure-preserving neural network-enhanced numerical methods for the Boltzmann equation. First, we target the moment approach, where a structure-preserving neural network will be employed to model the minimal entropy closure of the moment system. By enforcing convexity of the neural network, one can show, that the intrinsic structure of the moment system, such as hyperbolicity, entropy dissipation and positivity is preserved. Second, we develop a neural network approach to solve the Boltzmann equation directly at discrete particle velocity level. Here, a neural network is employed to model the difference between the full non-linear collision operator of the Boltzmann equation and the BGK model, which preserves the entropy dissipation principle. Furthermore, we will develop strategies to generate training data which fully sample the input space of the respective neural networks to ensure proper functioning models.
Participants
- Prof. Dr. Martin Frank
- Dr. Tianbai Xiao
- Steffen Schotthöfer
The Data-dependency Gap: A New Problem in the Learning Theory of Convolutional Neural Networks
Abstract
In Statistical learning theory, we aim to prove theoretical guarantees on the generalization ability of machine learning algorithms. The approach usually consists in bounding the complexity of the function class associated with the algorithm. When the complexity is small (compared to the number of training samples), the algorithm is guaranteed to generalize well. For neural networks however, the complexity is often times extremely large. Nevertheless, neural networks—and convolutional neural networks especially—have achieved unprecedented generalization in a wide range of applications. This phenomenon cannot be explained by standard learning theory. Although a rich body of literature provides partial answers through analysis of the implicit regularization imposed by the training procedure, the phenomenon is by large not well understood. In this proposal, we introduce a new viewpoint on the “surprisingly high” generalization ability of neural networks: the data-dependency gap. We argue that the fundamental reason for these unexplained generalization abilities may well lie in the structure of the data itself. Our central hypothesis is that the data acts as a regularizer on neural network training. The aim of this proposal is to verify this hypothesis. We will carry out empirical evaluations and develop learning theory, in the form of learning bounds depending on the structure in the data. Here we will connect the weights of trained CNNs with the observed inputs at hand, taking into account the structure in the underlying data distribution. We focus on convolutional neural networks, the arguably most prominent class of practical neural networks. However, the present work may pave the way for the analysis of other classes of networks (this may be tackled in the second funding period of the SPP).
Participants
- Prof. Dr. Marius Kloft
Towards a Statistical Analysis of DNN Training Trajectories
Abstract
Deep neural networks (DNNs) have become one of the state-of-the-art
machine learning methods in many areas of applications.
Despite this success and the fact that these methods have been
considered for around 40 years, our current statistical understanding
of their learning mechanisms is still rather limited.
Part of the reasons for this lack of understanding is the
fact that in many cases the tools of classical statistical
learning theory can no longer be applied.
The overall goal of this project is to establish key aspects of a
statistical analysis of DNN training algorithms that are close to
the ones used in practice. In particular, we will
investigate the statistical properties of trajectories produced by
(variants of) gradient descent, where the focus lies on the question
whether such trajectories contain predictors with good generalization
guarantees. From a technical perspective, reproducing kernel
Hilbert spaces, for example of the so-called neural tangent kernels,
play a central role in this project.
Participants
- Prof. Dr. Ingo Steinwart
- Max Schölpple
Towards everywhere reliable classification - A joint framework for adversarial robustness and out-of-distribution detection
Abstract
Adversarial robustness and out-of-distribution (OOD) detection have been treated
separately so far. However, the separation of these problems is
artificial as they are inherently linked to each other. Advances in adversarial robustness
generalizing beyond the threat models used at training time seem possible only
by going beyond the classical adversarial training framework proposed and merging
OOD detection and adversarial robustness in a single framework.
Participant
- Prof. Dr. Matthias Hein
Understanding Invertible Neural Networks for Solving Inverse Problems
Abstract
Designing and understanding models with tractable training, sampling, inference and evaluation
is a central problem in machine learning. In this project, we want to contribute to the fundamental understanding of invertible deep NNs that are used for solving inverse problems. We are interested in the posterior distribution of the unknown data in dependence on noisy samples from the forward operator of the inverse problem and some latent distribution. Based on realistic error estimates between the true posterior and its ,,reconstruction'' given by the invertible NN, we intend to address
- the influence of properties of the forward operator of the inverse problem as well as
- different latent distributions, e.g.\ uni- and multimodal ones, distributions with small variances or heavy tailed ones.
We have to address the question how to control Lipschitz constant of the inverse NN. Based on our theoretical insights, we then want to solve various real-world tasks.

Participants
- Prof. Dr. Gabriele Steidl
- Paul Hagemann

